在江苏公务员行测考试中,数学运算一直是常考题型。作为公认的具有一定难度的题目,在最近几年,尤其是随着报考公务员人数的剧增,数学运算开始担负起划分考生等级,选拔具有优秀思维能力公务人员的重任。因此数学运算的题量不仅有所增加,难度也逐步放开。考生要在原本就不多的时间内,进行读题、思考、计算等一系列解答过程,并迅速、准确的选择出所有题目的答案,没有一定的方法和技巧,显然是一项不可能完成的任务。
江苏公务员考试网(http://www.jsgwy.com.cn/)在整理近几年浙江真题的过程中,特意总结了几个具有普适性的解题方法,能够帮助考生快速找到思路、简化解题过程、优化计算步骤。
一、方程法
众所周知,方程法因其思考过程为正向思维,思路简单,故不需要复杂的分析。适用于公务员考试数学运算绝大部分题目,如行程问题、工程问题、盈亏问题、和差倍比问题、浓度问题、利润问题、年龄问题等均可以通过方程法来求解。但是方程法的明显缺陷是计算量较大、费时间。对此,我们可以通过优化未知数的设法和化简解方程的过程来提高解题速度。
1.巧设未知数
设未知数的原则:①设的未知数要便于理解,方便列方程;②尽量减少未知数的个数,方便解方程。具体而言,可以利用比例关系、取中间量等技巧优化未知数,达到便于列方程和解方程的目的。
【例题1】 募捐晚会售出300元、400元、500元的门票共2200张,门票收入84万元,其中400元和500元的门票张数相等。300元的门票售出多少张?
A.800 B.850 C.950 D.1000
解析:此题答案为D。设400和500元门票各卖了x张,300元门票卖了(2200-2x)张,则300×(2200-2x)+400x+500x=840000。解得x=600,300元的门票卖了2200-2×600=1000张,选D。
另解:400元和500元的门票张数相等,因此它们的平均价格应该为(400+500)÷2=450元,那么设300元的门票售出了x张,则400元和500元的门票共售出了2200-x张。由题意得,300x+450×(2200-x)=840000,解得x=1000,即300元的门票售了1000张。
要减少未知数的个数,必须找到未知数间的数量关系。参考例题1中对“400元和500元的门票张数相等”这样揭示未知数间数量关系的条件的处理。
2.巧解多元方程
当题中数量关系比较隐蔽,直接找出各个量之间的联系有困难时,可以设辅助未知数,实现由未知向已知的转化,这就是多元方程。
解多元方程主要采用消元的方法,即在解题过程中巧妙地将其消去,而并不需要求这些未知数。一般来说,消元通常是“求什么保留什么”,即消元时,尽量保留题目要求的未知量。此外,还可以通过整体法、换元法来解方程,以提高解方程组的效率。
【例题2】 某月刊杂志,定价2.5元,劳资处一些人订全年,其余人订半年,共需510元,如果订全年的改订半年,订半年的改订全年,共需300元,劳资处共多少人?
A.20 B.19 C.18 D.17
解析:此题答案为C。设原来订全年的有x人,原来订半年的有y人,则有
2.5×12x+2.5×6y=510…… ①
2.5×6x+2.5×12y=300…… ②
观察方程组,①中x,y的系数与②中x,y的系数正好对称,所以整体相加,可得2.5×18(x+y)=510+300,解得x+y=18。
3.利用数的特性解不定方程
所谓不定方程,是指未知数的个数多于方程个数,且未知数受到某些限制(如要求是有理数、整数或正整数等等)的方程或方程组。
随着公务员考试难度的不断加大,在解决数学运算问题的过程中,经常会出现不定方程的求解。其中以二元一次不定方程的几率最大,通用形式为ax+by=c,a、b、c为已知整数,x、y为所求自然数。不定方程的解不是唯一确定的,如果未知数的解不加限制条件,它会有无数种可能。因此在解这类方程时,我们需要利用整数的奇偶性、整除性、尾数特性等多种方法来缩小解的范围,最终得到答案。
【例题3】 工人甲一分钟可生产螺丝3个或螺丝帽9个,工人乙一分钟可生产螺丝2个或螺丝帽7个。现在两人各花了20分钟,共生产螺丝和螺丝帽134个。问生产的螺丝比螺丝帽多几个?
A.34个 B.32个 C.30个 D.28个
解析:此题答案为A。设工人甲生产螺丝x分钟,工人乙生产螺丝y分钟。则3x+2y+9(20-x)+7(20-y)=134,整理得6x+5y=186。6x、186是偶数,根据偶数+偶数=偶数,则确定5y是偶数,只有当5y的尾数是0时,才符合要求,故6x的尾数是6。x为1、6、11、16能满足条件,只有当x=16时y=18能满足y小于20。此时螺丝有3×16+2×18=84个,螺丝帽有134-84=50个,螺丝比螺丝帽多84-50=34个。
二、特殊值法
在公务员考试数学运算中,题干中给出的数字信息越来越少,需要考生通过阅读题干文字信息,摘取出有用的、关键的数量运算关系。此时,可以使用特殊值法,即在题目所给的范围内取一个恰当的特殊值直接代入,瞬间将复杂的问题简单化。
特殊值法必须选取满足题干的特殊数、特殊点、特殊函数、特殊数列或特殊图形代替一般的情况,并由此计算出结果,从而达到快速解题的目的。灵活地运用特殊值法能提高解题速度,增强解题的信心。在公务员考试中,特殊值法常应用于和差倍比问题、行程问题、工程问题、浓度问题、利润问题、几何问题等,几乎所有与方程有关的题目都可通过设特殊值来解决,也属于通用性较强的方法。
【例题4】 2010年末,某公司高收入员工(占20%)收入是一般员工(占80%)的6倍。未来5年实现员工总收入增加1倍,同时缩小收入差距,当一般员工收入增加1.5倍时,则高收入员工收入是一般员工的多少倍?
A.5 b.4.5 C.4 D.3
解析:此题答案为C。设高收入员工人数为1人,则一般员工为4人,设2010年末一般员工的工资为1元,则高收入员工工资为6元,总工资为1×4+6×1=10元。将题干中的数据填入下表中:

则高收入员工收入为(20-2.5×4)÷1=10元,是一般员工的10÷2.5=4倍,选C。
三、十字交叉法
十字交叉法是已知总的平均数,求两个部分的平均数或数量的一种简便方法,即求加权平均数的简便算法。这里的平均数可以是浓度、产量、价格、利润、增长率、速度等。正是由于加权平均数适用于任何题目环境,所以十字交叉法的考查几率较大。
十字交叉法一般只用于两个部分相关的平均值问题,且运用的前提已知总体平均值r。例如:
(1)男生与女生人数分别为A和B,男生的平均分是a,女生的平均分是b。全班的平均分是r。
(2)有A克浓度为a的盐水、B克浓度为b的盐水,混合后浓度为r。
(3)数量分别为A与B的人口,分别增长a与b,总体增长率为r。
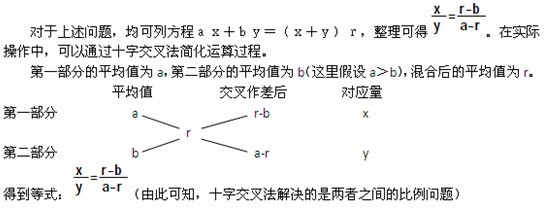
在运用十字交叉法进行计算时要注意:①总体平均数r总是介于部分平均数a与b之间;②当a、b表示增长率时,所求得的x和y是增长之前的数值。
【例题5】 某市气象局观测发现,今年第一、二季度本市降水量分别比去年同期增加了11%和9%,而两个季度降水量的绝对增量刚好相同。那么今年上半年该市降水量同比增长多少?
A.9.5% B.10% C.9.9% D.10.5%
解析:此题答案为C。利用十字交叉法,设该市上半年降水量总体增长为x%











