在公务员考试行测科目的数量关系模块中,“牛吃草”问题出现频率较高,一般是采取“公式法”来进行解题。但是大部分考生在记公式的过程中,容易记混,另外,在稍微复杂的问题面前,套公式也容易搞错。因此,江苏公务员考试网(http://www.jsgwy.com.cn/)就该问题进行详细解析,希望能给大家提供一点帮助。
一、公式法
牛吃草问题的经典公式:草场原有草量=(牛数-每天长草量)×天数
这个公式可以从追及问题的角度出发理解:追及距离=(大速度-小速度)×追及时间
在这个问题中,原有草量相当于追及距离,(牛每天吃草量-每天长草量)相当于(大速度-小速度),假设每头牛每天吃草量为1,则可写成(牛数-每天长草量),天数就是追及时间。所以,草场原有草量=(牛数-每天长草量)×天数
二、方程法
有些考生认为公式不好记,或者容易记混,则也可以从理解的角度简单地列出方程组:
草的消耗量=草的供应量,而草的消耗量就是牛吃草的总量,即
牛吃草的总量=草场供应草的总量,即
牛数×天数×每头牛每天吃草量=草场原有草量+新长草总量,即
牛数×天数×每头牛每天吃草量=草场原有草量+天数×每天新长草量
其中,“每头牛每天吃草数”、“草场原有草量”、“每天新长草量”均为未知数,它们之间的关系是比例关系,所以可以把“每头牛每天吃草量”设为1,“每天新长草量”设为x,“草场原有草量”设为y;则有:牛数×天数×1=y+天数×x
三、例题分析
【例1】 一牧场上的青草每天都匀速生长。这片青草可供27头牛吃6周,或供23头牛吃9周。那么可供21头牛吃几周?
【解析】
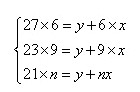
根据公式法,设所求天数为n,例1可以列出以下方程组:
从1、2个方程中解出x=15,y=72,代入第3个方程,可解出n=12
【例2】某车站在检票前若干分钟就开始排队,每分钟来的旅客人数一样多。从开始检票到等候检票的队伍消失,若同时开5个检票口则需30分钟,若同时开6个检票口则需20分钟。如果要使队伍 10分钟消失,那么需同时开几个检票口?
【解析】假设,开始检票前人数为y,每分钟新来人数为x,所求检票口为n,则有
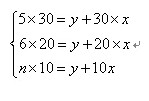
解出x=3,y=60,n=9
【例3】某海港货口不断有外洋轮船卸下货来,又不断用汽车将货物运走,如果用9辆车,12小时可以清场,如果用8辆车,16小时也可以清场。该厂开始只用3辆车,10小时之后又增加了若干辆车,再过4小时就已清场,那么后来增加的车数应是?
【解析】假设每小时卸货单位为x,原有存货量为y,后增加的车辆数为n,则:
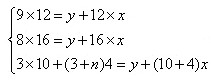
解出x=5,y=48,n=19
行测更多解题思路和解题技巧,可参看2013年公务员考试技巧手册。










