本节开始讲解排列组合可能会遇到的各类题型,首先是不包含特殊方法的基本题型。解答此类题型的时候注意分类全面、分步合理,做到不多不漏不重复,在保证准确率的前提下尽量提高解题速度,为难题预留更多的时间。
1,基础公式型
这类题比较简单,考生熟练排列组合基本技巧即可快速得到正确答案。
【例题1】
参加会议的人每两人都彼此握手,有人统计共握手36次,问与会人数为( )。
A.9B.10C.11D.12
【解析】
握手不分顺序,甲和乙握手与乙和甲握手没有区别,故不考虑排列,假设与会人数为N个,问题相当于从N个人中选出2个握手,共有多少种选法。则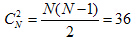 ,可求得N=9,故答案选A。
,可求得N=9,故答案选A。
2,分类讨论型
这类题考生需要将题设进行分类处理,分类切记全面具体,做到不多不漏,才能得到正确答案。
【例题2】
甲组有4名男员工,3名女员工;乙组有6名男员工、2名女员工。若从甲、乙两组中各选出2名员工,则选出的4人中恰有1名女员工的不同选法共有( )种。
A.180B.72C.252D.324
【解析】
分类讨论,
选出的1名女员工为甲组,则甲组还需从4名男员工选1名,乙组需要从6名男员工选2名,共有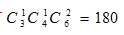 种;
种;
选出的1名女员工为乙组,则乙组还需从6名男员工选1名,甲组需要从4名男员工选2名,共有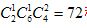 种。
种。
共有180+72=252种,所以答案选C。
3,分步讨论型
这类题考生需要将题设进行分布讨论,注意步骤与步骤之间不能交叉,最后运用乘法原理即可。
【例题3】
有甲、乙、丙三项任务,甲需2人承担,乙、丙各需1人承担。从10人中选派4人承担这三项任务,不同的选法共有( )。
A.1260种 B.2025种 C.2520种 D.5040种
【解析】
分步讨论,
第一步,先从10人中选出4人,共有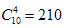 种;
种;
第二步,从选出的4人中选2人给甲,从剩下的2人中选1人给乙,另一人给丙,共有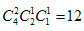 种;
种;
第三步,共有选法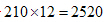 种,故答案选C。
种,故答案选C。
更多解题思路和解题技巧,可参看2016年公务员考试技巧手册。










