本节主要讲解排列组合中常见的使用特殊方法的综合题型。这类题如果采用枚举的方法,一步一步计算,思维复杂且计算量大;而一旦采用这一类标配特殊解法,不仅思路清晰,而且计算简便,对于解题效率来说无疑是一柄利器!
1,特殊优先原则
有一类题型,题设中某些元素的约束条件较多,属于特殊元素,为避免排序时重复性地删减去重,对特殊元素进行特别关照,即“特殊元素,优先处理,特殊位置,优先考虑”。
【例题1】
8人排成前后两排,每排4人,其中甲、乙在前排,丙在后排,共有多少排法?
【解析】
题干中甲、乙、丙属于特殊元素,优先处理。
先把甲、乙排在前排,共有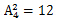 种可能的选择;再把丙排在后排,共有
种可能的选择;再把丙排在后排,共有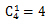 种可能的选择;最后其他人的位置没有特殊要求,共有
种可能的选择;最后其他人的位置没有特殊要求,共有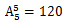 种排列。故总共有
种排列。故总共有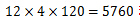 种排法。
种排法。
2,捆绑插空型
捆绑型:
排列时如果遇到要求几个元素相邻,则将它们捆绑起来当作1个元素,再与其他元素一起排列,并考虑捆绑元素内部的排列,此种方法称为“捆绑法”。
【例题2】
记者要为5名志愿都和他们帮助的2位老人拍照,要求排成一排,2位老人相邻但不排在两端,不同的排法共有( )种。
A.1440B.960C.720D.480
【解析】
首先2位老人要求相邻,则把2位老人捆绑为一组,内部可以排序,共有2种排列;然后把5人加这组排序,共有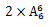 种排列;再剔除2位老人排在两端的排列,有
种排列;再剔除2位老人排在两端的排列,有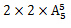 种排列,所以最终的结果是
种排列,所以最终的结果是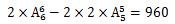 种,故答案选B。
种,故答案选B。
插空型:
排列时如果遇到要求几个元素不能相邻,则先把其他元素进行排列后,再把不能相邻的元素插入其他元素排列的空隙中去,此种方法称为“插空法”。
【例题3】
马路上有编号为1,2,3,4,5,6,7,8,9的九只路灯,现要关掉其中的3盏,但不能关掉相邻的2盏,也不能关掉两端的2盏,求满足条件的关灯方法有多少种?
【解析】
此题从正面入手分类较多,比较麻烦;可以考虑为,在6盏排成一列的亮的灯的空隙中,插入3盏不亮的灯,就满足要求了,空隙共有5个,则满足条件的方法共有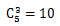 种。
种。
更多解题思路和解题技巧,可参看2016年公务员考试技巧手册。










