本节接着讲解排列组合中常见的特殊方法题型,有些题目从正面入手难度较大,解答此类题型时,不妨转换思路,活用技巧,从多个角度综合考虑,必能找到“突破口”,解题起来才能“势如破竹”。
3,分配插板型
如果题目中要求把n个元素分成m堆,且每堆至少有1个元素,可以看作把(m-1)个木板插入这n个元素形成的(n-1)个空隙中,即从(n-1)个空隙中选出(m-1)个空隙给个木板,之后可运用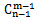 计算,此种方法称之为“分配插板法”。
计算,此种方法称之为“分配插板法”。
【例题1】
某单位订阅了30份学习资料发放给3个部门,每个部门至少发放9份材料。问一共有多少种不同的发放方法?( )
A.7B.9C.10D.12
【解析】
首先其中把24份资料发放给3个部门,每个部门发放8份,那么问题就变成了“6份资料发放给3个部门,每个部门至少发1份”;利用插板法,即是在5个空隙中选出2个,则共有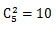 种发放方法。
种发放方法。
4,间接计算法
有些问题从正面考虑分类繁琐,计算量大,不宜采用,这时需考虑间接计算法。常见的方法有“先排列,再去多”和“先排列,再去重”两种。
(1)先排列,再去多
首先不管限制条件,直接对元素进行排列,最后在减去不满足条件的多余的排列,此种方法即为“先排列,再去多”。
【例题2】
从0,1,2,3,4,5,6,7,8,9这十个数字中取出三个数,使其和为不小于10的偶数,不同的取法有多少种?
【解析】
此题如果依次枚举,计算量较大,考虑“先排列,再去多”的方法。
先求出和为偶数的取法,和为偶数,则取出的3个数字要么3个偶数,要么1个偶数、2个奇数。3个偶数的取法有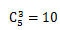 种,1偶2奇的取法有
种,1偶2奇的取法有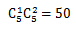 种,所以和为偶数的取法共有60种;
种,所以和为偶数的取法共有60种;
再求出和为小于10的偶数的取法,共有9个;
故满足题设的取法共有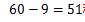 种。
种。
(2)先排列,再去重
同样,如果有些问题从正面难于枚举,可以考虑先不管限制条件进行排列,最后再除掉重复的排列数,此种方法即为“先排列,再去重”。
【例题3】
5男4女排成一排,要求男生必须按从高到矮的顺序,共有多少种不同的排列方法?
【解析】
先排列,9人排列,共有 种排列方法;
种排列方法;
再去重,假如男生从左往右从高到矮排列,只有一种方法,上述战法重复了 次,故只有
次,故只有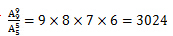 种排列方法;
种排列方法;
同理,男生从左往右从矮到高,也只有一种站法,也有3024种。故总共有6048种排列方法。
更多解题思路和解题技巧,可参看2016年公务员考试技巧手册。










