排列组合衍生出的概率题型也是公考的热门考点之一,本节主要讲解概率求解的问题。这类题型基于排列组合,但又有很多独有的特征和知识点,在公考中的热度不减。
1,概率的一般概念
概率:
概率即是所有事件中,事件A所占的比例,用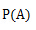 表示。
表示。
等可能事件的概率:
一次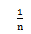 试验连同其可能出现的结果称为一个基本事件,通常一次试验中的某一事件A由若干个基本事件组成。如果一次试验中所有可能出现的结果有n个,那么每一个基本事件的概率都为;如果事件A包含的结果有m个,那么A出现的概率为
试验连同其可能出现的结果称为一个基本事件,通常一次试验中的某一事件A由若干个基本事件组成。如果一次试验中所有可能出现的结果有n个,那么每一个基本事件的概率都为;如果事件A包含的结果有m个,那么A出现的概率为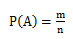 。
。
条件概率:
在事件B已经发生的前提下,事件A发生的概率成为条件概率,即A在B条件下的概率。记作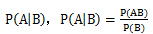 ,其中
,其中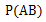 为事件AB同时发生的概率。
为事件AB同时发生的概率。
全概率公式:
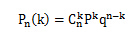 ,其中
,其中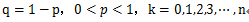 ,
,
2,例题
【例题1】
有5本不同的书,其中教科书2本,杂志2本,工具书1本。先将其随机排成一列,则同一类别的书都不相邻的概率是多少?
【解析】
先考虑同一类别的书相邻的排列数,
同一类别的书都相邻的排列数为 ;同一类别中有且仅有一种相邻的排列数为
;同一类别中有且仅有一种相邻的排列数为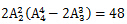 ;
;
再求出排列总数为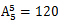 ;
;
故同一类别的书都不相邻的概率是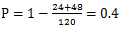 。
。
【例题2】
根据天气预报,未来4天中每天下雨的概率约为0.6,则未来4天中仅有1天下雨的概率p为( )。
A.0.03<p<0.05B.0.06<p<0.09
C.0.13<p<0.16D.0.16<p<0.36
【解析】
可作如下考虑:从4天中选取1天下雨,另外3天不下雨,应用全概率公式可得,,故答案选C。










