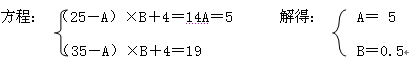1.我们知道,一个正方形可以剪成4个小正方形,那么一个正方形能否剪成9个正方形,能否剪成11个正方形(大小不一定要相同)?( )。
A.前者能、后者不能B.前者不能、后者能
C.两者都不能D.两者都能
2.某公司为了促销一种产品,推出一套价格方案,价格表如下:
|
一次性购买件数 |
1~10 |
11~50 |
51~100 |
101~300 |
300以上 |
|
每件价格(单位:元) |
37 |
32 |
30 |
27 |
25 |
现在某人有现金2900元,那么他最多可以购买这种产品的件数是多少?( )。
A.96B.97C.108D.107
3.某家庭某年一月份、二月份、三月份的煤气用量分别为4立方米、25立方米、35立方米,支付一月份、二月份、三月份的煤气费分别为4元、14元、19元。如果该市煤气费收费的方法是:煤气费=基本费用+超额费用+保险费,且若每月用气量不超过最低限度A立方米时,只收基本费用3元和每户每月定额保险费C元;若用气量超过A立方米,则超过的部分每立方米收取B元。又知道保险费不少于1元。若某用户四月份用气32立方米时,该用户这年四月份应该交纳的煤气费用是多少元?( )。
A.16B.16.5C.17D.17.5
4.长180厘米的绳子,从一端开始每3厘米做一记号,每4厘米也做一记号,然后将有记号的地方剪断,绳子共剪成多少段?( )。
A.105B.100C.95D.90
5.已知某数N除以45余12,则N的12倍除以45余数是多少?( )。
A.26B.19C.13D.9
参考答案解析
1.【答案】D。
2.【答案】D。解析:2900÷27=107余11。
3.【答案】D。解析:根据一月份的煤气费为4元,依据公式煤气费=基本费用+超额费用+保险费,其中基本费用3元,保险费C不少于1元可知,C=1元,基本费用为3元,由此可列方程
从而可知四月份32立方米应交纳(32-5)×O.5+4=17.5。
4.【答案】D。解析:3厘米做一个记号应有60处,4厘米做一个记号应有45处,如果在每个记号处剪断应有60+45=105段。但在每12厘米(3、4的最小公倍数处)处重合一次,故实际应有60+45-(180÷12)=90段。
5.【答案】D。解析:12×l2÷45=3余9。