1.一次校友聚会共有50人参加,在参加聚会的同学中,每个男生认识的女生人数各不相同,而且恰好构成一串连续的自然数,已知认识女生最少的一个男生认识15名女生,并有一名男生认识所有女生,则参加这次聚会的男生一共有( )
A.16名
B.17名
C.18名
D.19名
2.一个分数的分母扩大3倍,分子不变,分数值则( )。
A.缩小3倍
B.缩小30倍
C.扩大3倍
D.不变
3.小明每天必须做家务,做一天可得3元钱,做得特别好时每天可得5元钱,有一个月(30天)他共得100元,这个月他有( )天做得特别好。
A.2
B.3
C.5
D.7
4.某学校数学系的120名学生需要选修人文类的选修课,有三门课供学生选择,每人至少选择一门课。已知三门课的选修人数各不相同,选择文学欣赏课的人数最多,且恰为选择音乐欣赏课的人数的两倍,未选择电影欣赏课的为70人,问最多有多少人只选择了一门选修课?( )
A.112
B.114
C.116
D.118
5.如图,三个图形的周长相等,则a∶b∶c是多少?( )
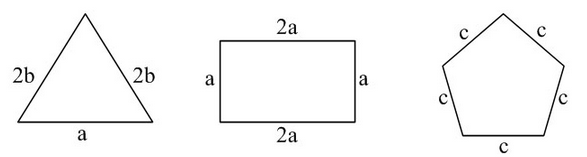
A.4∶5∶6
B.8∶10∶15
C.20∶25∶24
D.24∶25∶20
江苏公务员考试网(http://www.jsgwy.com.cn/)解析 题目或解析有误,我要纠错。
1.答案: C
解析: 设一共有男生x名,则有女生50-x名,由于每个男生认识的女生人数各不相同,且恰好构成一串连续的自然数,所以可得下列方程:(50-x)-15+1=x,解得x=18,故本题的正确答案为C。
2.答案: A
解析:
分数a/b分母扩大3倍变为a/3b,分数值缩小3倍。因此正确答案为A。
3.答案: C
解析:
设做得好的天数为n,则有5n+3(30-n)=100,解得n=5,故正确答案为C。
4.答案: C
解析: 最值问题。可知选择电影欣赏课的人数为50,选择文学欣赏课的人数至少为52人,选择音乐欣赏课的人数至少为26人,为了使得选一门课的人数尽可能地多,我们应该让选择一门以上课程的尽量选择三门课程,52+26+50-120=8,因此最少有4人选择不止一门选修课,最多有116人只选择了一门选修课。
5.答案: C
解析: