排列组合问题属于数学运算中必考的重难点，在近几年的国考、联考以及单独命题省考中每年均会考查。由于高中阶段我们学习的排列组合难度比较高，所以很多考生以为行测考试中排列组合的难度也是非常高的，实际上并非如此。只要掌握了公式、概念以及常见的方法，大多数题目都可以快速解答。
今天江苏公务员考试网（www.jiangsugwy.org）与大家一起来详细了解一下排列组合题型中常用到的插空法。插空法是公考排列组合题型中常用的重要方法之一，通过练习熟练掌握对应技巧后，能有效提高做题正确率，下面我们通过几道真题来详细了解一下如何运用插空法解题。
插空法解题
题型特征：题目中出现“间隔”“不相邻”“不连续”等限制条件
解题方法：
1.先排：先安排可以相邻的元素，形成若干个空位。
2.再插：将不相邻的元素插入到空位中。
例1.【2015国考】把12棵同样的松树和6棵同样的柏树种植在道路两侧，每侧种植9棵，要求每侧的柏树数量相等且不相邻，且道路起点和终点处两侧种植的都必须是松树。问有多少种不同的种植方法：
A. 36
B. 50
C. 100
D. 400
【解题思路】由题意，公路两边各6棵松树和3棵柏树，道路起点和终点处两侧种植的都必须是松树，那么中间有5个空，由于柏树要求互不相邻，故从5个空中选出3个空栽种柏树即可。故每一边的种植方式为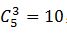
，故总共不同的种植方式为10×10=100种，正确答案为C。
【点评】因为树是相同的，因此不需要考虑顺序用C列式，如果题干给出的主体需要考虑顺序，则应用A列式。如果无法明确分辨，建议可从中选出两个元素调换位置，如果对结果没影响，用组合C;调换位置后变为新的情况，则与顺序有关用A。
例2.【2015黑龙江】小区内空着一排相邻的8个车位，现有4辆车随机停进车位，恰好没有连续空位的停车方式共有多少种?
A. 48
B. 120
C. 360
D. 1440
【解题思路】题目要求求出“恰好没有连续空位的停车方式有多少种”，即排列组合中“不相邻问题”，可使用插空法求解。四辆车停进四个不同的车位，共有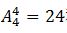
种方式。然后在四辆车空出的5个空当中选出4个，即可满足“没有连续空位的停车方式”，共
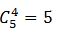种方式。则满足条件的停车方式一共有：24×5=120种，正确答案为B。
【点评】此类题目中，原有的一类元素里，部分元素的状态发生了改变，因此可将两种状态分别看作两类元素进行解题。
例3. 【2017江苏】两公司为召开联欢晚会，分别编排了3个和2个节目，要求同一公司的节目不能连续出场，则安排节目出场顺序的方案共有：
A. 12种
B. 18种
C. 24种
D. 30种
【解题思路】题目要求同一公司节目不能连续出场，则同一公司节目之间必然插入另一个公司节目，第一个公司3个节目之间刚好有2个空隙插入第二个公司的2个节目。先排第一个公司，3个节目出场顺序有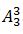
种情况;再将第二个公司的节目排入空隙，出场顺序有A_2^2种情况;所以节目出场顺序共有方案数为
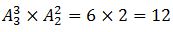，总共12种情况，正确答案为A。
【点评】此类题目中，两类元素都不相邻，先排其中一个元素，再用另一类元素插空，中间的空必须先占满。
例4.【2018四川下】某场学术论坛有6家企业作报告，其中A企业和B企业要求在相邻的时间内作报告，C企业作报告的时间必须在D企业之后、在E企业之前，F企业要求不能第一个，也不能最后一个作报告。如满足所有企业的要求，则报告的先后次序共有多少种不同的安排方式?
A. 12
B. 24
C. 72
D. 144
【解题思路】根据题意，按照先后次序，D、C、E三者相对顺序仅此1种;A、B要求相邻，利用捆绑法有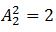
种，再插入D、C、E形成的空中，有
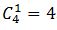种方法;F不是第一个，也不是最后一个，只能插入AB、D、C、E之间的3个空中，有
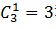种方法;分步用乘法，因此不同安排方式共1×2×4×3=24种，正确答案为B。
【点评】本题是捆绑法和插空法结合。出现“相邻”用捆绑法，先将需要相邻的AB捆绑，再进行后续的插空，最后分步用乘法得出总情况数即可。
排列组合题目虽有一定难度，但掌握了技巧也能快速解题。有舍有得，前提是有得到的能力，切勿将锦上添花的部分全盘放弃。
