国考的数量出现的点“新”、题“新”等“新”常态是值得大家去注意的，因为这意味着考查大家能力的方式又多了一种，大家在备考时就要多多注意这方面知识的积累。
所谓的点“新”就是在老题型上面结合“新”算法，旧壶装新酒。同时，还出现了一种“新”题型，根据题目要求判断未知量之间的关系图。江苏公务员考试一本通教材编辑部就在此为大家盘点一下国考出现的“新”考题。让大家有充足的准备去接住国考命题人放出的“大招”！
一、点“新”型
在今年数量的15道题中我们可以看到很多变形题，这些变形题是在原有题型的基础上结合了其他考点，比如：概率结合不等式的运算，几何结合统计方法，容斥结合多元方程组的代换。不同“旧”考点相互结合变成了一个“新”考题，一道题不再单纯考一个知识点，而是两个或两个以上的考点融合到一道题目中综合考查大家的能力，这就要求大家不能死记硬背运算公式了，要学会灵活运用，做到举一反三，才能应对国考以后要出现的点“新”题。
【例】
某单位原有几十名职员，其中有14名女性。当两名女职员调出该单位后，女职员的比重下降了3个百分点。现在该单位需要随机选派两名职员参加培训，问选派的两人都是女职员的概率在以下哪个范围内（ ）
A.小于1% B.1%~4%
C.4%~7% D.7%~10%
【解析】
设单位原有总人数为x，根据题目条件可得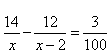
，先考虑x除以7余0、除以3余2，可得x=21m+14。当x=35时，
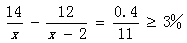；当x=56时，
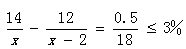所以x介于35-56之间，再考虑x为10的倍数。当x=50时满足， 
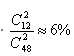，C项符合。
【总 结】
本题考查是概率问题，我们需掌握的基本公式：P（A）=
但是本题你单单掌握这个公式是远远不够的，我们根据题目条件列出方程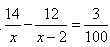
，这个方程如果解出来，必然耗费大量时间。因此我们就要学会巧用不等式
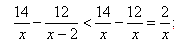最快速锁定答案范围x≤66，同时根据方程的倍数特性可得：x应为100的倍数，开始使用赋值法，假设x=60时，不符合；假设x=50时，恰好满足。根据排列组合可得：满足条件A的情况数就是
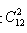，总的情况数
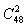。P（A）6％。C项当选。
【举一反三】
本题的点“新”在概率、排列组合、方程法联合不等式运算方法、赋值法这几个相结合。对于国考出现“点”新型的考题，笔者在这里就不一一例举了，大家可以好好总结今年数量15道题，就不难发现类似于这种老考点融合成“新”考点的题目不在少数。而在以后的省考、联考等公务员考试中，数量关系这一模块会越来越多的考查大家对各个知识点的综合把握和灵活运用的能力。学宝云课堂的老师要求大家看到一道题后，清楚此题的基础题型后，不能拘泥于单个知识点的解题方法，要学会综合运用多个知识点相结合去解题。
二、题“新”型
2015年、2016年国考连续出现了看图题，何谓看图题，就是要求考生根据题目条件所给出的未知量之间的关系，通过选项A、B、C、D给出的图象，进行判断未知量的关系符合哪一个图象。这是国考出现的新题型，它不隶属于任何一个考点，但是任何考点都能出此题型。此类题目更能综合的考查大家的能力，提高区分度。因此大家在备考时需要多多在意这类题目，对这方面的知识进行积累。
【例】
某集团三个分公司共同举行技能大赛，其中成绩靠前的X人获奖。如获奖人数最多的分公司获奖的人数为Y，问以下哪个图形能反映Y的上、下限分别与X的关系（ ）
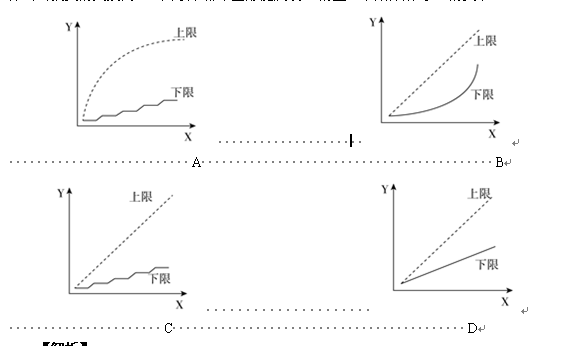
【解析】
获奖人数最多的分公司获奖人数Y的上、下限即Y的最大值、最小值。①考虑上限，当X人全部来自同一个分公司时，Y=X。A项错误。②考虑下限，当X=1时，此时Y=X=1；当X=2时，Y的下限为1，三个分公司获奖人数为1、1、0；当X=3时，Y的下限为1，三个分公司获奖人数为1、1、1。观察发现C项图形最符合Y与X的变化趋势，当选。
【总结】
对于这个题目大多考生是手足无措的，因为从开始就没明白此类题目要求是什么，再加上选项所给出的图形这么抽象，所以考场上大部分考生的选择就是交给上帝去解决。本题要求的是Y的上、下限分别与X的关系，也就是求Y的最大值、最小值分别是多少。此题运用假设最值的思想，假设Y取最大值时，Y=X是正比例函数，很显然A项首先排除。假设Y取最小值， Y=1，X=1、2、3。就是三个公司都有一个人获奖，因此可以得出Y的下限是一个与X轴呈阶段性平行的图形，答案自然就选择C项。
【举一反三】
2015年国考副省级考试中曾经出现过类似这样的题，在今年地市级和副省级又出现了，并且难度要比去年大了许多。可见以后国考这类题型将会在数量关系这一模块中长此立足。判断关系趋势图难度是有的，但是只要大家仔细审题，利用假设最值等等方法，排除错误选项。验证正确选项，不难将此题收入囊中。
学宝云课堂的老师提醒大家：认真总结历年国考省考中出现的题型和考点，牢牢掌握各个知识点，对于国考的数量出现的点“新”、题“新”等“新”常态，要以不变应万变。多留意加强这方面知识的积累。只有用知识将自己的风帆满满的鼓起，才能“长风破浪会有时，直挂云帆济沧海”！
